Share
Click for larger version (PNG); click for PDF version. Click here for the list of dolls.
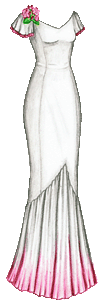
Got started a little late today, so this dress isn’t my favorite, but it’s reasonably cute, I think. It’s supposed to be in the style of 1930s evening gowns, although it’s not based on any one dress. (So as always with the historical costumes that I pretty much make up, take the style, color, etc. with a grain of salt.) The rhododendrons come from some pictures my dad posted on Facebook of wild rhododendrons blooming around my family’s property on Hood Canal. Whenever I go to visit I always seem to miss seeing them bloom, so it’s nice to have pictures at least!
Every day that goes by makes me feel crueler and crueler. Someone, guess the answer soon! A couple people have come really close, but the exact number is still a mystery. But at least you know it’s under 1000 and — OK, above 200. I know, that’s not really much help…
Question: How many Prismacolor pencils do I own as of May 18th?
This includes the ones that I use, all the stubby little pencils that are too short for my current sharpener but I just can’t toss, all the ones I have in reserve and my set of Verithin pencils I hardly ever use.
Just to restate the rules:
1) It’s a new year, so even if you’ve already won one, feel free to guess again.
2) One guess per person per post.
3) If no one gets the exact number by noon EST, May 25th, I’ll pick the closest guess.
It is great to see you back to posting everyday. Visting your site is part of my daily routine. I check my email, check this site and a few others everyday. I sometimes visit this site several times a day. You have a phenominal talent.
this dress is so beautiful, i love it! i check your site every day, i love all your drawings.
I’m going to guess maybe 752 Prismacolor pencils :)
keep up your amazing work, the routine youve got going is perfect!
463 pencils, and that’s a totally random guess.
372?
I love this dress! It’s the simple ones that are my favorite. This one is elegant and seems like something someone shy, beautiful and really sweet would wear. I don’t know. It seems every outfit you make has a story hidden inside the colored folds there seems to be a vivid personality etched into your art.
I’m going to guess you have 463.
So pretty! I wish I had a dress like this.
I guess 500
312.
336
417
How about 746?
Beautiful, I would love to wear this – maybe as a wedding dress??
490 (going lower this time)
I love the dress :)
New number then: 396
724?!
ˆ random guess ^.^
anyway, your dress is really pretty! you should maybe start a dress series inspired by different plants and flowers :D
I love the dress the colouring is so delicate!
Is the number 146?
615
I love this dress!
Another random guess, is that allowed?
638
This is really really pretty. 567
679 is my guess. Wow did you have to hunt down all your little pencil stubs to count them?
Thanks, I’m really glad people like this one, I wasn’t crazy about it when I finished it so it cheers me up :)
Katie, I’ve got them all in their own little bag. In some respects my Prismacolor sanity is intact ;)
im gonna guess 872. this dress is AMAZING!!! i would totally wear it!!
1,000-ish?
450
Beautiful dress! I wish I owned one like it :)
On a soon to come Mermaid Monday, do you think you could make a mermaid costume for me? I’m thinking something very flowy and kelp-y looking, but in blues and greens and purples, with a traditional sort of tail. I just made my first paper mache mermaid and she is sparkley silver/white with aluminum foil coils for hair and a light purple sparkley tail. I coated her whole body in a thin layer of fabric paint.
Wow! This is gorgeous! Hummm… I’ll guess 287.
I think I ‘ll guess 324. I really like this dress. Did you ever see the new Alice in Wonderland? There are a lot of great costumes in it.
I love it!!!! im going to guess….500
Oh my, I’ve missed a lot of outfits! It’s great to see you back and drawing, Liana!
This dress is beautiful. I love the way the pink and white fade into each other at the bottom of the skirt. And the detail on the flower? You never cease to amaze me. :)
and I guess I’ll toss a number in here too: 542
I love this one! I’ll guess 673.
I just love your dresses, you are so talented.
my guess for your pencils is 827.
This has to be one of my favorite dresses of yours. it has a certain soft, delicate charm to it, and the person who wears it would be very graceful, i would think. Hmm, yesterday i did 530, the day before i did 615….so today I’ll try 445.
*Gasp* Oh! Pretty pretty pretty. You are so evil cause now I want to make this dress really really bad.
Guess 800
Hmmm… This is hard! Err… 777!
Love this! Is it wrong I totally want to be married in it? Lets see…..pencils….42…no actually 542.
I love your dolls and dresses. I only which I could draw something like this.
Let’s see how many pencils you’ve got, perhapas 879?
Noon EST on the 25th has passed, contest is over! Please see the most recent blog post.
738 :D